SOLVED EXAMPLES1. The motor of an engine is rotating about its axis with an angular velocity of 100 rev/minute. It comes to rest in 15 s, after being switched off. Assuming constant angular deceleration, calculate the number of revolutions made by it before coming to rest.

2. Starting from rest, a fan takes five seconds to attain the maximum speed of 400 rpm (revolution per minute). Assuming constant acceleration, find the time taken by the fan in attaining half the maximum speed.

3. A bucket is being lowered down into a well through a rope passing over a fixed pulley of radius 10 cm. Assume that the rope does not slip on the pulley. Find the angular velocity and angular acceleration of the pulley at an instant when the bucket is going down at a speed of 20 cm/s and has an acceleration of 4.0 m/s2.

4. Consider a pulley fixed at its centre of mass by a clamp. A light rope is wound over it and the free end is tied to a block. The tension in the rope is T. (a) Write the forces acting on the pulley. How are they related? (b) locate the axis of rotation. (c) Find the torque of the forces about the axis of rotation.
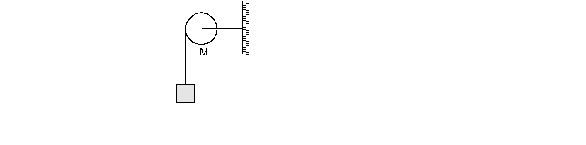
Sol.(a) The forces on the pulley are (figure)
(i) attraction by the earth, Mg vertically downward,
(ii) tension T by the rope, along the rope,
(iii) contact force N by the support at the centre N = T + Mg (centre of mass of the pulley is at rest, so Newton’s 1st law applies).
(b) The axis of rotation is the line through the centre of the pulley and perpendicular to the plane of the pulley.
(c) Let us take the positive direction of the axis towards the reader.
The forces Mg passes through the centre of mass and it intersects the axis of rotation. Hence the torque of Mg about the axis is zero (Case- II). Similarly, the torque of the contact force N is also zero.
The tension T is along the tangent of the rim in the vertically downward direction. The tension and the axis of rotation are perpendicular but never intersect. Case III applies. Join the point where the rope leaves the rim to the centre. This line is the common perpendicular to the tension and the axis. Hence the torque is T.r (positive, since it will try to rotate the pulley anticlockwise).
5. A wheel of radius 10 cm can rotate freely about its centre as shown in figure. A string is wrapped over its rim and is pulled by a force of 5.0 N. It is found that the torque produces an angular acceleration 2.0 rad/s in the wheel. Calculate the moment of the wheel.

Sol. The forces acting on the wheel are (i) W due to gravity, (ii) N due to the support at the centre and (iii) F due to tension. The torque of W and N are separately zero and that of F is F.r. The net torque is
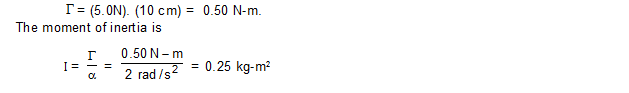
6. A wheel is rotating at an angular speed w about its axis which is kept vertical. An identical wheel initially at rest is gently dropped into the same axle and the two wheels start rotating with a common angular speed. Find this common angular speed.

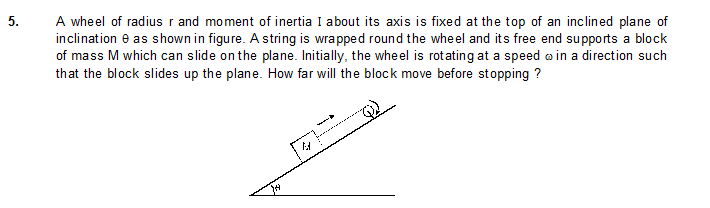
7. A wheel of moment of inertia I and radius r is free to rotate about its centre as shown in figure. A string is wrapped over its rim and a block of mass m is attached to the free end of the string. The system is released from rest. Find the speed of the block as it descends through a height h.

8. Consider a light rod with two heavy mass particles at its ends. Let AB be a line perpendicular to the rod as shown in figure. What is the moment of inertia of the system ab 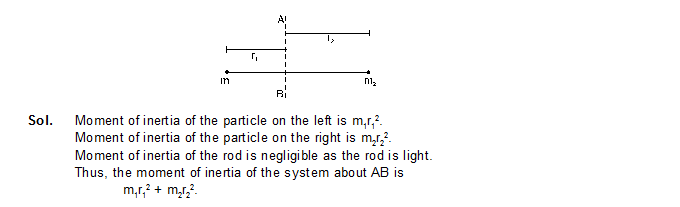
9. Three particles, each of mass m, are situated at the vertices of an equilateral triangle ABC of side L (figure). Find the moment of inertia of the system about the line AX perpendicular to AB in the plane of ABC.

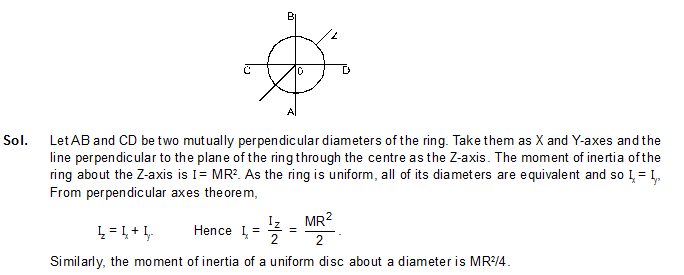
10. Find the moment of inertia of a uniform ring of mass M and radius R about a diameter.
11. Find the moment of inertia of a solid cylinder of mass M and radius R about a line parallel to the axis of the cylinder and on the surface of the cylinder.
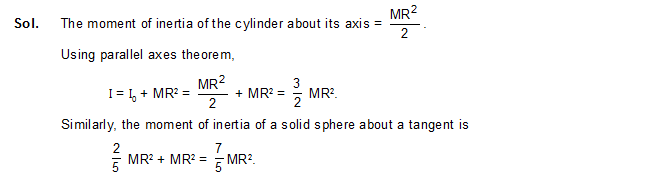
12. A uniform sphere of mass 200 g rolls without slipping on a plane surface so that its centre moves at a speed of 2.00 cm/s. Find its kinetic energy.
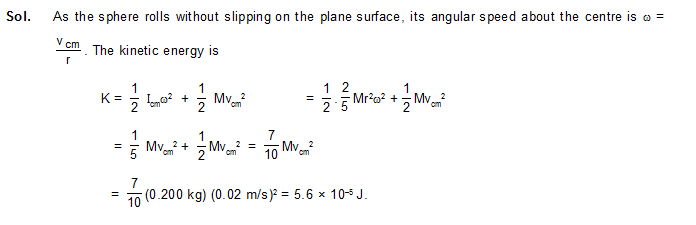
1. Can an object be in pure translation as well as in pure rotation ?
2. A simple pendulum is a point mass suspended by a light thread from a fixed point. The particle is displaced towards one side and then released. It makes small oscillations. Is the motion of such a simple pendulum a pure rotation ? If yes, where is the axis of rotation?
4. A ball is whirled in a circle by attaching it to a fixed point with a string. Is there an angular rotation of the ball about its centre ? If yes, is this angular velocity of the ball about the fixed point ?
5. The moon rotates about the earth in such a way that only one hemisphere of the moon faces the earth. Can we ever see the “other face” of the moon from the earth ? Can a person on the moon ever see all the faces of the earth ?
6. The torque of the weight of any body about any vertical axis is zero. Is it always correct ?

8. A heavy particle of mass m falls freely near the earth’s surface. What is the torque acting on this particle about a point 50 cm east to the line of motion. Does this torque produce any angular acceleration in the particle ?
9. If several forces act on a particle, the total torque on the particle may be obtained by first finding the resultant force and then taking torque of this resultant. Prove this. Is this result valid for the forces acting on different particles of a body in such a way that their lines of action intersect at a common point ?
10. If the sum of all the forces acting on a body is zero, is it necessarily in equilibrium ? If the sum of all the forces on a particles is zero, is it necessarily in equilibrium?
11. If the angular momentum of a body is found to be zero about a point, is it necessary that it will also be zero about a different point ?
12. If the resultant torque of all the forces acting on a body is zero about a point, is it necessary that it will be zero about any other point ?
13. A body is in translational equilibrium under the action of coplanar forces. If the torque of these forces is zero about a point, is it necessary that it will also be zero about any other point?
14. A rectangular brick is kept on a table with a part of its length projecting out. It remains at rest if the length projected is slightly less than half the total length but it falls down if the length projected is slightly more than half the total length. Given reason.
15. When a fat person tries to touch his toes, keeping the legs straight, he generally falls, Explain with reference to figure.

16. A ladder is resting with one end on a vertical wall and the other end on a horizontal floor. It is more likely to slip when a man stands near the bottom or near the top ?
17. When a body is weighed on an ordinary balance we demand that the arm should be horizontal if the weights one the two pans are equal. Suppose equal weights are put on the two pans, the arm is kept at an angle with the horizontal and released. Is the torque of the two weights about the middle point (point of support) zero ? Is the total torque zero ? If so, why does the arm rotate and finally become horizontal?
18. The density of a rod AB continuously increases from A to B. Is it easier to set it in rotation by clamping it at A and applying a perpendicular force at B or by clamping it at B and applying the force at A ?
19. When tall buildings are constructed on earth, the duration of day-night slightly increases. Is it true ?
20. If the ice at the poles melts and flows towards the equator, how will it affect the duration of day-night ?
21. A hollow sphere, a solid sphere, a disc and a ring all having same mass and radius are rolled down on an inclined plane. If no slipping takes place, which one will take the smallest time to over a given length ?
22. A sphere rolls on a horizontal surface. Is there any point of the sphere which has a vertical velocity ?
.png)

3. A particle moves with a constant velocity parallel to the X-axis. Its angular momentum with respect to the origin
(A) is zero (B*) remains constant
(C) goes on increasing (D) goes on decreasing
5. Figure shows a small wheel fixed coaxially on a bigger one of double the radius. The system rotates about the common axis. The strings supporting A and B do not slip on the wheels. If x and y be the distances travelled by A and B in the same time interval, then
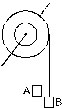
(A) x = 2y (B) x = y (C*) y = 2 x (D) none of these
6. A body is rotating uniformly about a vertical axis fixed in an inertial frame. The resultant force on a particle of the body not on the axis is -
(A) vertical (B) horizontal and skew with the axis
(C*) horizontal and intersecting the axis (D) none of these
7. A body is rotating nonuniformly about a vertical axis fixed in an inertial frame. The resultant force on a particle of the body not on the axis is -
(A) vertical (B*) horizontal and skew with the axis
(C) horizontal and intersecting the axis (D) none of these


10. A uniform rod is kept vertically on a hroizontal smooth surface at a point O. If it is rotated slightly and released, it falls down in the horizontal surface. The lower end will remain
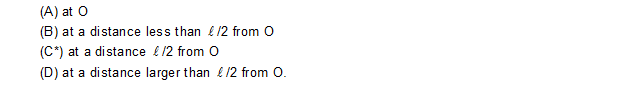
11. A circular disc A of radius r is made from an iron plate of thickness t and another circular disc b of radius 4r is made from an iron plate of thickness t/4. The relation between the moments of inertia IA and IB is
(A) IA > IB (B) IA = IB (C*) IA < IB
(D) depends on the actual values of t and r.
12. Equal torques act on the disc A and B of the previous problem, initially both being at rest. At a later instant, the linear speeds of a point on the rim of A and another point on the rim of B are vA and vB respectively. We have
(A*) vA > vB (B) vA = vB (C) vA < vB
(D) the relation depends on the actual magnitude of the torques.
13. A closed cylindrical tube containing some water (not filling the entire tube) lies in a horizontal plane. If the tube is rotated about a perpendicular bisector, the moment of inertia of water about the axis
(A*) increases (B) decreases (C) remains constant
(D) increases if the rotation is clockwise and decreases if it is anticlockwise.
14. The moment of inertia of a uniform semicircular wire of mass M and radius r about a line perpendicular to the plane of the wire through the centre is -
(A*) Mr2 (B) 1/2 Mr2 (C) 1/4 Mr2 (D) 2/5Mr2.
15. Let I1 and I2 be the moments of inertia of two bodies of indentical geometrical shape, the first made of aluminium and the second of iron.
(A*) I1 < I2 (B) I1 = I2 (C) I1 > I2
(D) relation between I1 and I2 depends on the actual shapes of the bodies
16. A body having its centre of mass at the origin has three of its particles at (a, 0, 0), (0, a, 0), (0, 0, a). The moments of inertia of the body about the X and Y axes are 0.20 kg-m2 each. The moment of inertia about the z-axis -
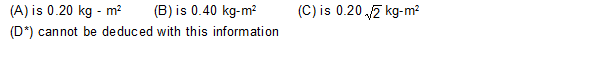


19. A person sitting firmly over a rotating stool has his arms stretched. If the folds his arms, his angular momentum about the axis of rotation
(A) increases (B) decreases (C*) remains unchanged (D) doubles
20. The centre of a wheel rolling on a plane surface moves with a speed v0. A particle on the rim of the wheel at the same level as the centre will be moving at speed

21. A wheel of radius 20 cm is pushed to move it on a rough horizontal surface. It is found to move through a distance of 60 cm on the road during the time it completes one revolution about the centre. Assume that the linear and the angular accelerations are uniform. The frictional force acting on the wheel by the surface is -
(A*) along the velocity of the wheel (B) opposite to the velocity of the wheel
(C) perpendicular to the velocity of the wheel (D) zero
22. The angular velocity of the engine (and hence of the wheel) of a scooter is proportional to the petrol input per second. The scooter is moving on a frictionless road with uniform velocity. If the petrol input is increased by 10%, the linear velocity of the scooter is increased by
(A) 50% (B) 10% (C) 20% (D*) 0%
23. A solid sphere, a hollow sphere and a disc, all having same mass and radius, are placed at the top of a smooth incline and released. Least time will be taken in reaching the bottom by -
(A) the solid sphere (B) the hollow sphere
(C) the disc (D*) all will take same time
24. A solid sphere, a hollow sphere and a disc, all having same mass and radius, are placed at the top of an incline and released. The friction coefficients between the objects and the incline are same and not sufficient to allow pure rolling. Least time will be taken in reaching the bottom by
(A) the solid sphere (B) the hollow sphere
(C) the disc (D*) all will take same time.
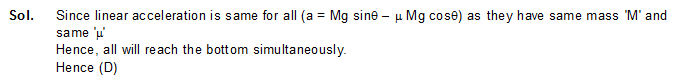
25. In the previous question, the smallest kinetic energy at the bottom of the incline will be achieved by
(A) the solid sphere (B*) the hollow sphere
(C) the disc (D) all will achieve same kinetic energy.
Sol. For all the bodies, torque is same .
Hence, angular momentum (L) is also same.
Now, K.E. = 1/2 mv2 + L2/2I
Linear velocity 'v' is same for all as same force acts on them.
Therefore more value of moment of inertia implies lesser
kinetic energy.
Among all, the hollow sphere has the maximum moment of inertia I = .2/3 MR2
Hence (B).
26. A string of negligible thickness is wrapped several times around a cylinder kept on a rough horizontal surface. A man standing at a distance from the cylinder holds on end of the string and pulls the cylinder towards him (figure). There is no slipping anywhere. The length of the string passed through the hand of the man while the cylinder reaches his hands is

1. The axis of rotation of a purely rotating body
(A) must pass through the centre of mass (B*) may pass through the centre of mass
(C) must pass through a particle of the body (D*) may pass through a particle of the body.
2. Consider the following two equations

In non inertial frames
(A) both A and B are true (B*) A is true but B is false
(C) B is true but A is false (D) both A and B are false
3. A particle moves on a straight line with a uniform velocity. Its angular momentum
(A) is always zero
(B*) is zero about a point on the straight line
(C*) is not zero about a point away from the straight line
(D*) about any given point remains constant
4. If there is no external force acting on a nonrigid body, which of the following quantities must remain constant ?
(A*) angular momentum (B*) linear momentum
(C) kinetic energy (D) moment of inertia
5. Let IA and IBbe moments of inertia of a body about two axes A and B respectively. The axis A passes through the centre of mass of the body but B does not.
(A) IA < IB (B) IA < IB, the axes are parallel
(C*) if the axes are parallel, IA < IB (D) if the axes are not parallel, IA >= IB
6. A sphere is rotating about a diameter.
(A) the particles on the surface of the sphere do not have any linear acceleration
(B*) the particles on the diameter mentioned above do not have any linear acceleration
(C) different particles on the surface have different angular speeds
(D) all the particles on the surface have same linear speed
7. The density of a rod gradually decreases from one end to the other. It is pivoted at an end so that it can move about a vertical axis through the pivot. A horizontal force F is applied on the free end in a direction perpendicular to the rod. The quantities, that do not depend on which end of the rod is pivoted, are
(A) angular acceleration
(B) angular velocity when the rod completes on rotation
(C) angular momentum when the rod completes one rotation
(D*) torque of the applied force
8. Consider a wheel of a bicycle rolling on a level road at a linear speed v0 (figure)
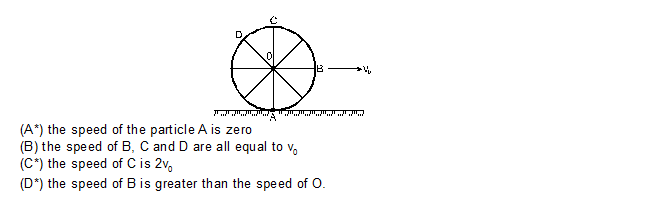
9. Two uniform solid spheres having unequal masses and unequal radii are released from rest from the same height on a rough incline. If the sphere roll without slipping,
(A) the heavier sphere reaches the bottom first
(B) the bigger sphere reaches the bottom first
(C*) the two spheres reach the bottom together
(D) the information given is not sufficient to tell which sphere will reach the bottom first.
10. A hollow sphere and a solid sphere having same mass and same radii are rolled down a rough inclined plane.
(A) the hollow sphere reaches the bottom first
(B*) the solid sphere reaches the bottom with greater speed
(C) the solid sphere reaches the bottom with greater kinetic energy
(D) the two spheres will reach the bottom with same linear momentum
11. A sphere cannot roll on
(A) a smooth horizontal surface (B*) a smooth inclined surface
(C) a rough horizontal surface (D) a rough inclined surface
12. In rear-wheel drive cars, the engine rotates the rear wheels and the front wheels rotate only because the car moves. If such a car acceleration on a horizontal road, the friction
(A*) on the rear wheels is in the forward direction
(B*) on the front wheels is in the backward direction
(C*) on the rear wheels has larger magnitude than the friction on the front wheels
(D) on the car is in the backward direction
(A) it will stay at rest
(B) it will make pure translational motion
(C*) it will translate and rotate about the centre
(D) the angular momentum of the sphere about its centre will remain constant
14. A sphere is rolled on a rough horizontal surface. It gradually slows down and stops. The force of friction tries to
(A*) decrease the linear velocity (B*) increase the angular velocity
(C) increase the linear momentum (D) decrease the angular velocity
(A*) it will continue pure rolling (B) it will slip down the plane
(C) its linear velocity will increase (D) its linear velocity will decrease
1. A wheel rotates with a constant acceleration of 2.0 rad/s2. If the wheel starts from rest, how many revolutions will it make in the first 10 seconds?
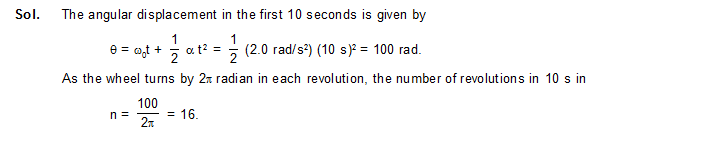
2. The wheel of a motor, accelerated uniformly from rest, rotates through 2.5 radian during the first second. Find the angle rotated during the next second.

3. A wheel having moment of inertia 2 kg-m2 about its axis, rotates at 50 rpm about this axis. Find the torque that can stop the wheel in one minute.
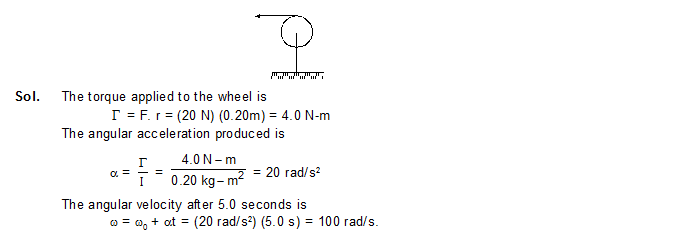
4. A string is wrapped around the rim of a wheel of moment of inertia 0.20 kg-m2 and radius
20 cm. The wheel is free to rotate about its axis. Initially, the wheel is at rest. The spring is now pulled by a force of 20 N. Find the angular velocity of the wheel after 5.0 seconds.

6. The pulley shown in figure has a moment of inertia I about its axis and its radius is R. Find the magnitude of the acceleration of the two blocks. Assume that the string is light and does not slip on the pulley.

7. Two small kids weighing 10 kg and 15 kg are trying to balance a seesaw of total length 5.0 m, with the fulcrum at the centre. If one of the kids is sitting at an end, where should the other sit?
Sol. It is clear that the 10 kg kid should sit at the end and the 15 kg kid should sit closer to the centre. Suppose his distance from the centre is x. As the kids are in equilibrium, the normal force between a kid and the seesaw equals the weight of that kid. Considering the rotational equilibrium of the seesaw, the torque of the forces acting on it should add to zero. The forces are
(a) (15 kg) g downward by the 15 kg kid,
(b) (10 kg) g downward by the 10 kg kid,
(c) weight of the seesaw and
(d) the normal force by the fulcrum.
Taking torques about the fulcrum,
(15 kg)g x = (10 kg)g (2.5 m)
or, x = 1.7 m.
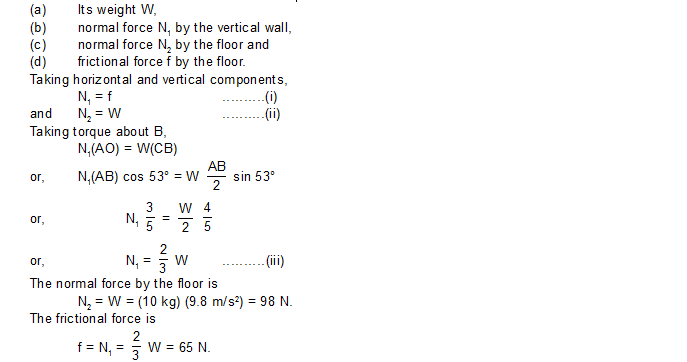




13. A uniform circular disc of mass 200 g and radius 4.0 cm is rotated about one of its diameter at an angular speed of 10 rad/s. Find the kinetic energy of the disc and its angular momentum about the axis of rotation.

14. A wheel rotating at an angular speed of 20 rad/s is brought to rest by a constant torque in 4.0 seconds. If the moment of inertia of the wheel about the axis of rotation is 0.20 kg -m2, find the work done by the torque in the first two seconds.
Sol. The angular deceleration of the wheel during the 4.0 seconds may be obtained by the equation

15. Two masses M and m are connected by a light string going over a pulley of radius r. The pulley is free to rotate about its axis which is kept horizontal. The moment of inertia of the pulley about the axis is I. The system is released from rest. Find the angular momentum of the system when the mass M has descended through a height h. The string does not slip over the pulley.
Sol. 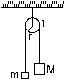
The situation is shown in figure. Let the speed of the masses be v at time t. This will also be the speed of a point on the rim of the wheel and hence the angular velocity of the wheel at time t will be v/r. If the height descended by the mass M is h, the loss in the potential energy of the “masses plus the pulley”
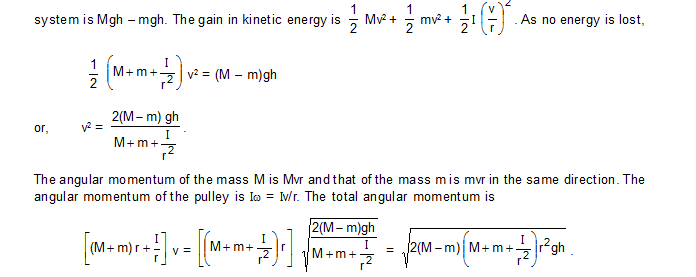
16. Figure shows a mass m placed on a frictionless horizontal table and attached to a string passing through a small hole in the surface. Initially, the mass moves in a circle of radius r0 with a speed v0 and the free end of the string is held by a person. The person pulls on the string slowly to decrease the radius of the circle to r. (a) Find the tension in the string when the mass moves in the circle of radius r. (b) Calculate the change in the kinetic energy of the mass.
Sol. The torque acting on the mass m about the vertical axis through the hole is zero. The angular momentum about this axis, therefore, remains constant. If the speed of the mass is v when it moves in the circle of radius r, when have
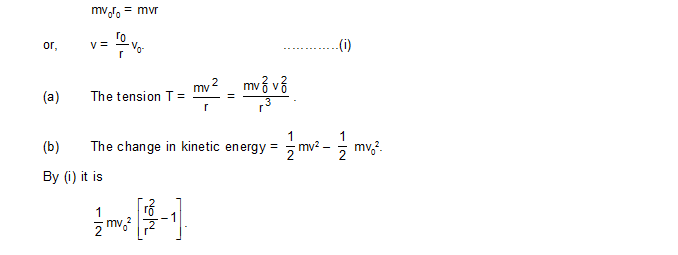

18. Four particles each of mass m are kept at the four corners of a square of edge a. Find the moment of inertia of the system about a line perpendicular to the plane of the square and passing through the centre of the square.
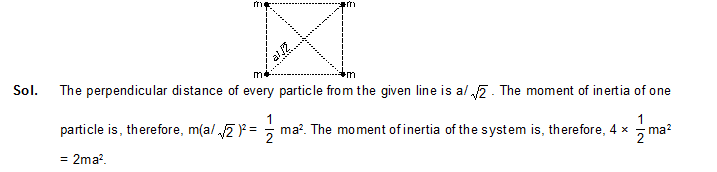
19. Two identical spheres each of mass 1.20 kg and radius 10.0 cm are fixed at the ends of a light rod so that the separation between the centres is 50.0 cm. Find the moment of inertia of the system about an axis perpendicular to the rod passing through its middle point.
20. Two uniform identical rods each of mass M and lengthare joined to form a cross as shown in figure. Find the moment of inertia of the cross about a bisector as shown dotted in the figure.

21. A uniform rod of mass M and length a lies on a smooth horizontal plane. A particle of mass m moving at a speed v perpendicular to the length of the rod strikes it at a distance a/4 from the centre and stops after the collision. Find (a) the velocity of the centre of the rod and (b) the angular velocity of the rod about its centre just after the collision.
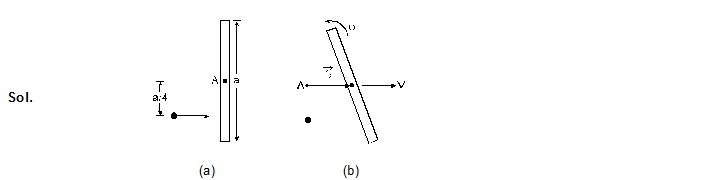
(a) (b)
The situation is shown in figure. Consider the rod and the particle together as the system. As there is no external resultant force, the linear momentum of the system will remains constant. Also there is no resultant external torque on the system and so the angular momentum of the system about the any line will remain constant.
Suppose the velocity of the centre of the rod is V and the angular velocity about the centre is w.

22. A wheel of perimeter 220 cm rolls on a level road at a speed of 9 km/h. How many revolutions does the wheel make per second ?





26. A cylinder of mass m is suspended through two strings wrapped around it as shown in figure. Find (a) the tension T in the string and (b) the speed of the cylinder as it falls through a distance h.

27. A force F acts tangentially at the highest point of a sphere of mass m kept on a rough horizontal plane. If the sphere rolls without slipping, find the acceleration of the centre of the sphere.

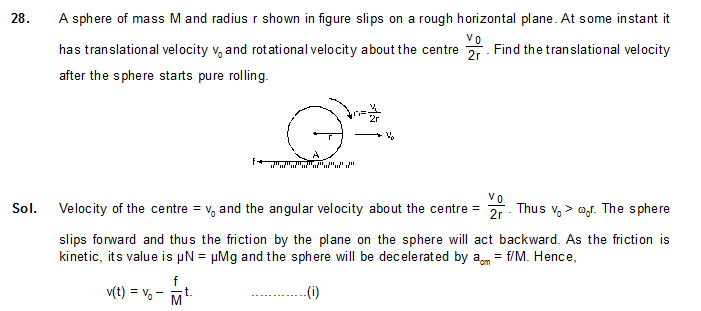
28. A sphere of mass M and radius r shown in figure slips on a rough horizontal plane. At some instant it has translational velocity v0 and rotational velocity about the centre . Find the translational velocity after the sphere starts pure rolling.

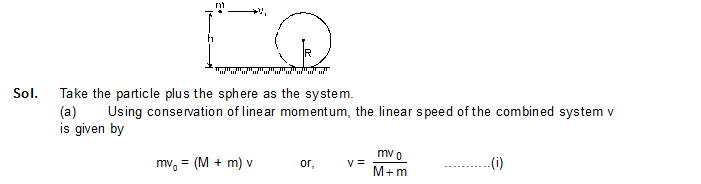
29. The sphere shown in figure lies on a rough plane when a particle of mass m travelling at a speed v0 collides and sticks with it. If the line of motion of the particle is at a distance h above the plane, find (a) the linear speed of the combined system just after the collision, (b) the angular speed of the system about the centre of the sphere just after the collision and (c) the value of h for which the sphere starts pure rolling on the plane. Assume that the mass M of the sphere is large compared to the mass of the particle so that the centre of mass of the combined system is not appreciably shifted from the centre of the sphere.

1. A wheel is making revolutions about its axis with a uniform angular acceleration. Starting from rest, it reaches 100 rev/sec in 4 seconds. Find the angular acceleration. Find the angle rotated during these four seconds.

2. A wheel rotating with uniform angular acceleration covers 50 revolutions in the first five seconds after the start. Find the angular acceleration and the angular velocity at the end of five seconds.

3. A wheel starting from rest is uniformly accelerated at 4 rad/s2 for 10 seconds. It is allowed to rotate uniformly for the next 10 seconds and is finally brought to rest in the next 10 seconds. Find the total angle rotated by the wheel.
3. 800 rad
4. A body rotates about a fixed axis with an angular acceleration of one radian/second. Through what angle does it rotate during the time in which its angular velocity increases from 5 rad/s to 15 rad/s.
4. 100 rad
5. Find the angular velocity of a body rotating with an acceleration of 2 re/s2 as it completes the 5th revolution after the start.

6. A disc of radius 10 cm is rotating about its axis at an angular speed of 20 rad/s. Find the linear speed of
(a) a point on the rim,
(b) the middle point of a radius
6. 2 m/s, 1 m/s
7. A disc rotates about its axis with a constant angular acceleration of 4 rad/s2. Find the radial and tangential accelerations of a particle at a distance of 1 cm from the axis at the end of the first second after the disc starts rotating.
7. 16 cm/s2, 4 cm/s2
8. A block hangs from a string wrapped on a disc of radius 20 cm free to rotate about its axis which is fixed in a horizontal position. If the angular speed of the disc is 10 rad/s at some instant, with what speed is the block going down at that instant ?
8. 2 m/s
9. Three particles, each of mass 200 g, are kept at the corners of an equilateral triangle of side 10 cm. Find the moment of inertia of the system about an axis [HCV_Chp 10_Ex_9]
(a) joining two of the particles and
(b) passing through one of the particles and perpendicular to the plane of the particles.
9. 1.5 × 10–3 kg-m-3, 4.0 × 10–3 kg-m3
10. Particles of masses 1 g, 2 g, 3 g,.........100 g are kept at the marks 1 cm, 2 cm, 3 cm,...... 100 cm respectively on a metre scale. Find the moment of inertia of the system of particles about a perpendicular bisector of the metre scale.
10. 0.43 kg-m2
11. Find the moment of inertia of a pair of spheres, each having a mass m and radius r, kept in contact about the tangent passing through the point of contact. [HCV_Chp 10_Ex_11]
11. 14mr2/5
12. The moment of inertia of a uniform rod of mass 0.50 kg and length 1 m is 0.10 kg -m2 about a line perpendicular to the rod. Find the distance of this line from the middle point of the rod.
12. 0.34 m
13. Find the radius of gyration of a circular ring of radius r about a line perpendicular to the plane of this line from the middle point of the rod.
![]()
14. The radius of gyration of a uniform disc about a line perpendicular to the disc equals its radius. Find the distance of the line from the centre.
![]()
15. Find the moment of inertia of a uniform square plate of mass m and edge a about one of its diagonals.
15. ma2/12



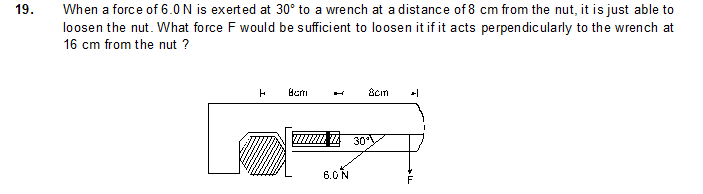
19. 1.5 N
20. Calculate the total torque acting on the body shown in figure about the point O.
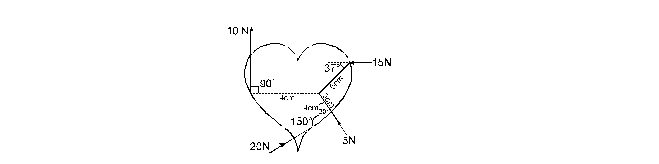
20. 0.54 N

22. A rod of mass m and length L, lying horizontally , is free to rotate about a vertical axis through its centre. A horizontal force of constant magnitude F acts on the rod at a distance of L/4 from the centre. The force is always perpendicular to the rod. Find the angle rotated by the rod during the time t after the motion starts.
22. 3Ft2/2ml
23. A square plate of mass 120 g and edge 5.0 cm rotates about one of the edges. If it has a uniform angular acceleration of 0.2 rad/s2, what torque acts on the plate ?
23. 2.0 × 10–5 N-m
24. Calculate the torque on the square plate of the previous problem if it rotates about a diagonal with the same angular acceleration.
24. 0.5 × 10–5 N-m
25. A flywheel of moment of inertia 5.0 kg -m2 is rotated at a speed of 60 rad/s. Because of the friction at the axle, it comes to rest in 5.0 minutes. Find (a) the average torque of the friction, (b) the total work done by the friction and (c) the angular momentum of the wheel 1 minute before it stops rotating.
25. (a) 1.0 N-m (b) 9.0 kJ (c) 60 kg-m2/s
26. Because of the friction between the water in oceans with the earth’s surface, the rotational kinetic energy of the earth is continuously decreasing. If the earth’s angular speed decreases by 0.0016 rad/day in 100 years, find the average torque of the friction on the earth. Radius of the earth is 6400 km and its mass is 6.0 × 1024 kg.
26. 5.8 × 1020 N-m
27. A wheel rotating at a speed of 600 rpm (revolutions per minute) about its axis is brought to rest by applying a constant torque for 10 seconds. Find the angular deceleration and the angular velocity 5 seconds after the application of the torque.
27. 1 rev/s2, 5 rev/s
28. A wheel of mass 10 kg and radius 20 cm is rotating at an angle speed of 100 rev/min when the motor is turned off. Neglecting the friction at the axle, calculate the force that must be applied tangentially to the wheel to bring it to rest in 10 revolutions.
28. 0.87 N
29. A cylinder rotating at an angular speed of 50 rev/s is brought in contact with an identical stationary cylinder. Because of the kinetic friction, torques act on the two cylinders, accelerating the stationary one and decelerating the moving one. If the common magnitude of the acceleration the stationary one and decelerating the moving one. if the common magnitude of the acceleration and deceleration be one revolution per second square, how long will it take before the two cylinders have equal angular speed ?
29. 25 s
30. A body rotating at 20 rad/s is acted upon by a constant torque providing it a deceleration of 2 rad/s2. At what time will the body have kinetic energy same as the initial value if the torque continues to act?
30. 20 s
31. A light rod of length 1 m is pivoted at its centre and two masses of 5 kg and 2 kg are hung from the ends as shown in figure. Find the initial angular acceleration of the rod assuming that it was horizontal in the beginning.

32. Suppose the rod in the previous problem has a mass of 1 kg distributed uniformly over its length.
(a) Find the initial angular acceleration of the rod.
(b) Find the tension in the supports to the blocks of mass 2 kg and 5 kg.
32. 8.0 rad/s2, 27.6 N, 29 N
33. Figure shows two blocks of mass m and M connected by a string passing over a pulley. The horizontal table over which the mass m slides is smooth. The pulley has a radius r and moment of inertia I about its axis and it can freely rotate about this axis. Find the acceleration of the mass M assuming that the string does not slip on the pulley.
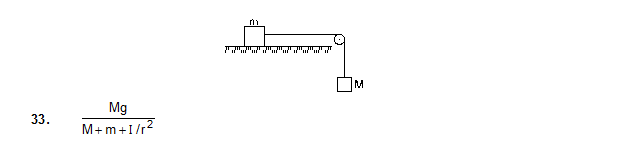
34. A string is wrapped on a wheel of moment of inertia 0.20 kg -m2 and radius 10 cm and goes through a light pulley to support a block of mass 2.0 kg as shown in figure. Find the acceleration of the block.

35. Suppose the smaller pulley of the previous problem has its radius 5.0 cm and moment of inertia 0.10 kg-m2. Find the tension in the part of the string joining the pulleys.
35. 6.3 N
36. The pulleys in figure are identical, each have a radius R and moment of inertia I. Find the acceleration of the block M.
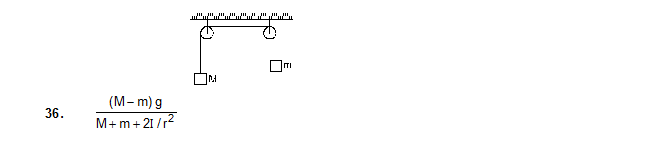 .
.
37. The descending pulley shown in figure has a radius 20 cm and moment of inertia 0.20 kg-m2. The fixed pulley is light and the horizontal plane frictionless. Find the acceleration of the block if its mass is 1.0 kg. Assume that there is no sliding between string and pulleys. The movable pulley is uniform disc.
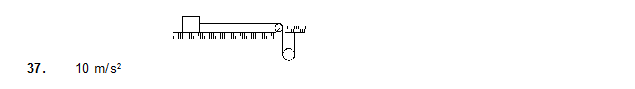
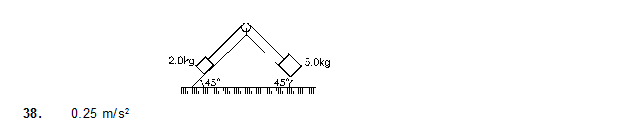
38. The pulley shown in figure has a radius 10 cm and moment of inertia 0.5 kg-m2 about its axis. Assuming the inclined planes to be frictionless, calculate the acceleration of the 4.0 kg block.
39. Solve the previous problem if the friction coefficient between the 2.0 kg block and the plane below it is 0.5 and the plane below the 4.0 kg block is frictionless.
39. 0.125 m/s2
40. A uniform metre stick of mass 200 g is suspended from the ceiling through two vertical strings of equal lengths fixed at the ends. A small object of mass 20 g is placed on the stick at a distance of 70 cm from
the left end. Find the tensions in the two strings.
40. 1.04 N in the left string and 1.12 N in the right

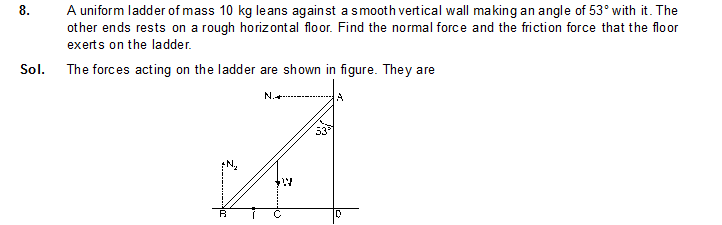
42. Suppose the friction coefficient between the ground and the ladder of the previous problem is 0.540. Find the maximum weight of a mechanic whose could go up and do the work from the same position of the ladder.
42. 44.0 kg
43. A 6.5 m long ladder rests against a vertical wall reaching a height of 6.0 m. A 60 kg man stands half way up the ladder. (a) Find the torque of the force exerted by the man on the ladder about the upper end of the ladder. (b) Assuming the weight of the ladder to be negligible as compared to the man and assuming the wall to be smooth, find the force exerted by the ground on the ladder.
43. (a) 740 N-m (b) 590 N vertical and 120 N horizontal
44. The door of an almirah is 6 ft high, 1.5 ft wide and weighs 8 kg. The door is supported by two hinges situated at a distance of 1 ft from the ends. If the magnitudes of the forces exerted by the hinges on the door are equal, find this magnitude.
44. 43 N
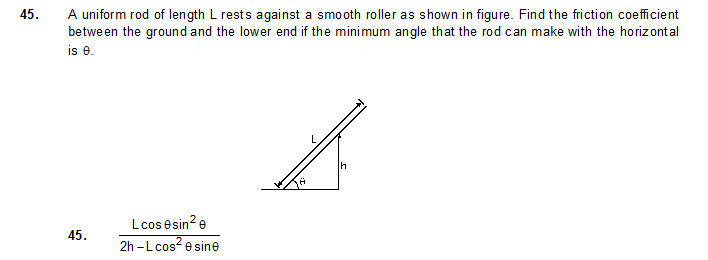
46. A uniform rod of mass 300 g and length 50 cm rotates at a uniform angular speed of 2 rad/s about an axis perpendicular to the rod through an end. Calculate (a) the angular momentum of the rod about the axis of rotation, (b) the speed of the centre of the rod and (c) its kinetic energy.
46. (a) 0.05 kg-m2/s (b) 50 cm/s (c) 0.05 J
47. A uniform square plate of mass 2.0 kg and edge 10 cm rotates about one of its diagonals under the action of a constant torque of 0.10 N.m. Calculate the angular momentum and the kinetic energy of the plate at the end of the fifth second after the start.
47. 0.5 kg-m2/s, 75 J
48. Calculate the ratio of the angular momentum of the earth about its axis due to its spinning motion to that about the sun due to its orbital motion. Radius of the earth = 6400 km and radius of the orbit of the earth about the sun = 1.5 × 108 km.
48. 2.66 × 10–7

50. A dumb-bell consists of two identical small balls of mass 1/2 kg each connected to the two ends of a 50 cm long light rod. The dumb-bell is rotating about a fixed axis through the centre of the rod and perpendicular to it at an angular speed of 10 rad/s. An impulsive force of average magnitude 5.0 N acts on one of the masses in the direction of its velocity for 0.10 s. Find the new angular velocity of the system.
50. 12 rad/s
51. A wheel of moment of inertia 0.500 kg-m2 and radius 20.0 cm is rotating about its axis at an angular speed of 20.0 rad/s. It picks up a stationary particle of mass 200 g at its edge. Find the new angular speed of the wheel.
51. 19.7 rad/s
52. A diver having a moment of inertia of 6.0 kg-m2 about an axis through its centre of mass rotates at an angular speed of 2 rad/s about this axis. If he folds his hands and feet to decrease the moment of inertia to 5.0 kg-m2, what will be the new angular speed ?
52. 2.4 rad/s
53. A boy is seated in a revolving chair revolving at an angular speed of 120 revolutions per minute. Two heavy ball from part of the revolving system and the boy can pull the balls closer to himself or may push them apart. If by pulling the balls closer, the boy decrease the moment of inertia of the system from 6 kg-m2 to 2 kg-m2, what will be the new angular speed ?
53. 360 rev/minute
54. A boy is standing on a platform which is free to rotate about its axis. The boy holds an open umbrella in his hand. The axis of the umbrella coincides with that of the platform. The moment of inertia of the “the platform plus the boy system” is 3.0 × 10–3 kg -m2 and that of the umbrella is 2.0 × 10–3 kg-m2. The boy starts spinning the umbrella about the axis at an angular speed of 2.0 rev/s with respect to himself . Find the angular velocity imparted to the platform.
54. 0.8 rev/s
55. A wheel of moment of inertia 0.10 kg-m2 is rotating about a shaft at an angular speed of 160 rev/minute. A second wheel is set into rotation at 300 rev/minute and is coupled to the same shaft so that both the wheels finally rotate with a common angular speed of 20 rev/minute. Find the moment of inertia of the second wheel.
55. 0.04 kg-m2
56. A kid of mass M stands at the edge of a platform of radius R which can be freely rotated about its axis. The moment of inertia of the platform is I. The system is at rest when a friend throws a ball of mass m and the kid catches it. If the velocity of the ball is v horizontally along the tangent to the edge of the platform when it was caught by the kid, find the angular speed of the platform after the event.
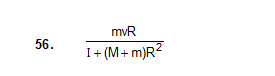
57. Suppose the platform of the previous problem is brought to rest with the ball in the hand of the kid standing on the rim. The kid throws the ball horizontally to this friend in a direction tangential to the rim with a speed v as seen by his friend. Find the angular velocity with which the platform will start rotating.
57. mvR/I+MR2


60. A uniform rod of length L lies on a smooth horizontal table. A particle moving on the table strikes the rod perpendicularly at an end and stops. Find the distance travelled by the centre of the rod by the time it turns through a right angle.

61. Suppose the particle of the previous problem has a mass m and a speed v before the collision and it sticks to the rod after the collision. The rod has a mass M. (a) Find the velocity of the centre of mass C of the system constituting “the rod plus the particle”. (b) Find the velocity of the particle with respect to C before the collision. (c) Find the velocity of the rod with respect to C before the collision (d) Find the angular momentum of the particle and of the rod about the centre of mass C before the collision. (e) Find the moment of inertia of the system about the vertical axis through the centre of mass C after the collision. (f) Find the velocity of the center of mass C and the angular velocity of the system about the centre of mass after the collision.
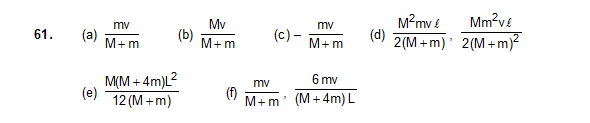

63. Two small balls A and B, each of mass m, are joined rigidly to the ends of a light rod of length L (figure). The system translates on a frictionless horizontal surface with a velocity v0 in a direction perpendicular to the rod. A particle P of mass m kept at rest on the surface sticks to the ball A as the ball collides with it. Find
(a) the linear speeds of the balls A and B after the collision, (b) the velocity of the centre of mass C of the system A + B + P and (c) the angular speed of the system about C after the collision.
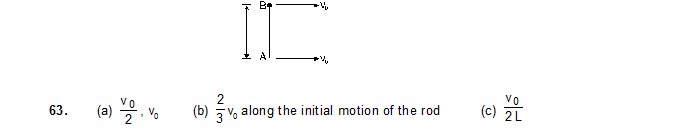
64. Suppose the rod with the balls A and B of the previous problem is clamped at the centre in such a way that is can rotate freely about a horizontal axis through the clamp. The system is kept at rest in the horizontal position. A particle P of the same mass m is dropped from a height h on the ball B. The particle collides with B and sticks to it. (a) Find the angular momentum and the angular speed of the system just after the collision. (b) What should be the minimum value of h so that the system makes a full rotation after the collision.

65. Two blocks of masses 400 g and 200 g are connected through a light string going over a pulley which is free to rotate about its axis. The pulley has a moment of inertia 1.6 × 10–4 kg-m2 and a radius 2.0 cm. Find (a) the kinetic energy of the system as the 400 g block falls through 50 cm (b) the speed of the blocks at this instant.
65. (a) 0.98 J (b) 1.4 m/s
66. The pulleys shown in figure has a radius of 20 cm and moment of inertia 0.2 kg-m2. The string going over it attached at one end to a vertical spring of spring constant 50 N/m fixed from below, and supports a 1 kg mass at the other end. The system is released from rest with the spring at its natural length. Find the speed of the block when it has descended through 10 cm. Take g = 10 m/s2.
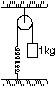
66. 0.5 m/s
67. A metre stick is held vertically with one end on a rough horizontal floor. It is gently allowed to fall on the floor. Assuming that the end at the floor does not slip, find the angular speed of the rod when it hits the floor.
67. 5.4 rad/s
68. A metre stick weighing 240 g is pivoted at its upper end in such a way that it can freely rotate in a vertical plane through this end (figure). A particle of mass 100 g is attached to the upper end of the stick through a light string of length 1 m. Initially, the rod is kept vertical and the spring horizontal when the system is released from rest. The particle collides with the lower end of the stick and sticks there. Find the maximum angle through which the stick will rise.

.png)
70. A cylinder rolls on a horizontal plane surface. If the speed of the centre is 25 m/s, what is the speed of the highest point ?
70. 50 m/s
71. A sphere of mass m rolls on a plane surface. Find its kinetic energy at an instant when its centre moves with speed v.
71. 7/10mv2
72. A string is wrapped over the edge of a uniform disc and the free end is fixed with the ceiling. The disc moves down, unwinding the string. Find the downward acceleration of the disc.
72. 2/3g
73. A small spherical ball is released from a point at a height h on a rough track shown in figure. Assuming that it does not slip anywhere, find its linear speed when it rolls on the horizontal part of the track.

74. A small disc is set rolling with a speed v on the horizontal part of the track of the previous problem from right to left. Two what height will it climb up the curved part ?
74. 3v2/4g
75. A sphere starts rolling down an incline of inclination q. Find the speed of its centre when it has covered a distance .


77. A solid sphere of mass m is released from rest from the rim of a hemispherical cup so that it rolls along the surface. If the rim of the hemisphere is kept horizontal, final the normal force exerted by the cup on the ball when the ball reaches the bottom of the cup.
77. 17 mg/7
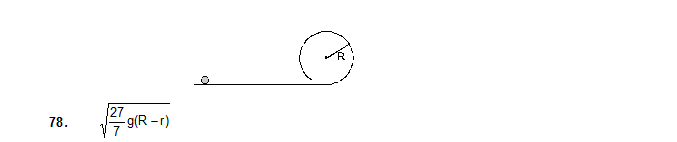
78. Figure shows a rough track, a portion of which is in from of a cylinder of radius R. With what minimum linear speed should a sphere of radius r be set rolling on the horizontal part so that it completely goes round the circle on the cylindrical part.
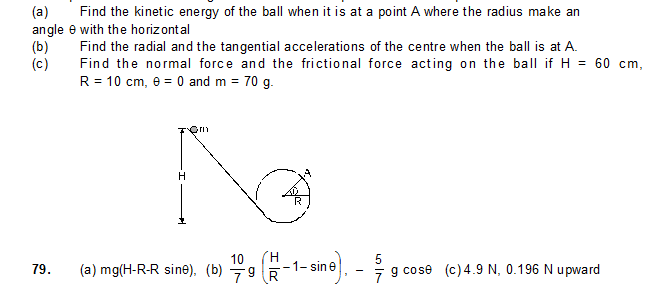
79. Figure shows a small spherical ball of mass m rolling down the loop track. The ball is released on the linear portion at a vertical height H from the lowest point. The circular part shown has a radius R.
80. A thin spherical shell of radius R lying on a rough horizontal surface is hit sharply and horizontally by a cue. Where should it be hit so that the shell does not slip on the surface?
80. 2R/3 above the centre

82. A thin spherical shell lying on a rough horizontal surface is hit by a cue in such a way that the line of action passes through the centre of the shell. As a result, the shell starts moving with a linear speed v without any initial angular velocity. Find the linear speed of the shell after it starts pure rolling on the surface.
82. 3v/5
83. A hollow sphere of radius R lies on a smooth horizontal surface. It is pulled by a horizontal force acting tangentially from the highest point. Find the distance travelled by the sphere during the time it makes one full rotation.
83. 
84. A solid sphere of mass 0.50 kg is kept on a horizontal surface. The coefficient of static friction between the surfaces in contact is 2/7. What maximum force can be applied at the highest point in the horizontal direction so that the sphere does not slip on the surface?
84. 3.3 N
85. A solid sphere is set into motion on a rough horizontal surface with a linear speed v in the forward direction and an angular speed v/R in the anticlockwise direction as shown in figure. Find the linear speed of the sphere (a) when it stops rotating and (b) when slipping finally ceases and pure rolling starts.

85. (a) 3 v/5 (b) 3 v/7
86. A solid sphere rolling on a rough horizontal surface with a linear speed v collides elastically with a fixed, smooth, vertical wall. Find the speed of the sphere after it has started pure rolling in the backward direction.
86. 3 v/7